广州童程童美少儿编程第七期大咖讲座《编程中的数学》精华笔录

01

半斤八两与编程中的进制

半斤八两这个耳熟能详的成语，往往用来形容两个事物不相上下，实力相当。但为什么半斤和八两是一样的呢？后如果把这个问题放到计算机编程中来看就能够理解了，其实这个成语是一个很酷的数学问题——进制。

进制是什么？我们举个例子。提起十二这个数字时，我们第一反应是它应该写成“12”；而在罗马数字中， 十二应该写成“XII”，其中X表示10，I表示1，II表示2。如同十二写成12或XII, 数字有着各种不同的计数法，12是阿拉伯数字的计数法。这种阿拉伯的计数法，我们一般称之为10进制的计数法。

所谓10进制， 便是逢十进位的意思， 比如十进制只有10个数：0，1，2，3，4，5，6，7，8，9。9以上到了十，就是进一位，就是10。而10就不是一个数字了，而是由两个数字组成。

如下图所示，用十进制拆解3508这个数字，则3表示 “1000的个数”、5表示“100的个数”、0表示“10的个数”、8表示“1的个数”。

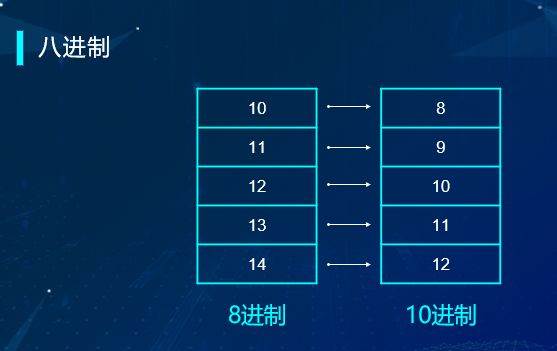
既然可以有10进制，自然也可以有8进制。按照10进制的方式，8进制就是逢八进一，所以应该是这样：0，1，2，3，4，5，6，7，到8时就是写成10，因为见到8，就得进位了。所以8进制的10，和10进制的8相等。8进制的11，就和10进制的9相等，八进制的12，就是十进制的10相等。

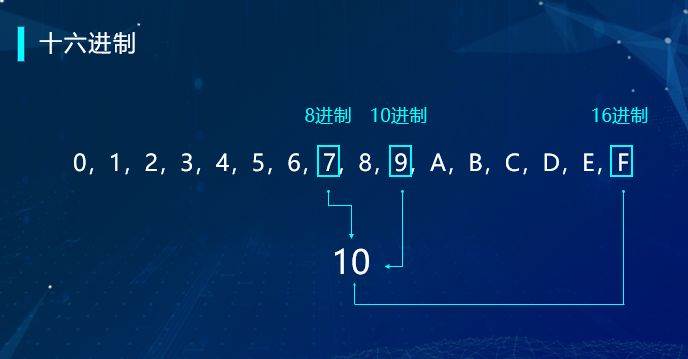
以此类推，可以存在任何进制，但通常十六进制比较常用。我们来看看十六进制，0，1，2，3，4，5，6，7，8，9，A, B, C, D, E, F……其中，A等同于十进制中的10，B等同于十进制中的11，而到F时需要进位成10，等同于十进制中的10。

我们回到上文提到的半斤八两问题，古时的十六两秤就是用的十六进制原则，因此“半斤=八两”。

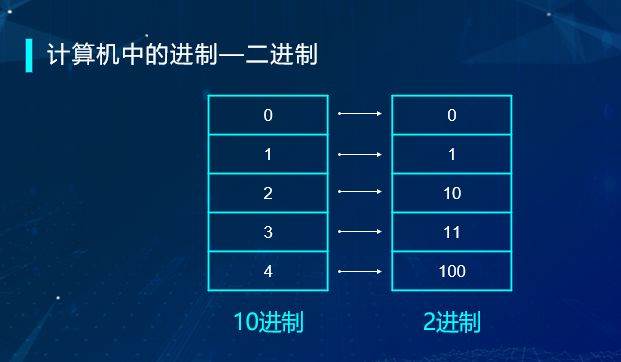
为什么学编程时学了进制呢？因为计算机保存数据为了便利使用二进制，因此二进制中我们只能看到数字0和1。

计算机中大量使用集成电路来处理数据。集成电路是由非常多的三极管组成的，如果一个三极管通电了，那么它代表1；不通电了，则代表0。

比如我们要保存一个数据5， 那么它转换成二进制就是101，用三个三极管就可以表示了，第一个三极管有电，第二个没电，第三个有电。

计算机可以把符合人类阅读习惯的十进制利用程序转换成二进制，但是字符A、B、C……汉字、图像又如何用二进制表达呢？计算机有一套自己的计算系统，我们称之为字库，当输入相应指令时，计算机会调用相应的字库，比如英文字母A是通过堆叠A的图形来实现的。

02

一切从“0”开始

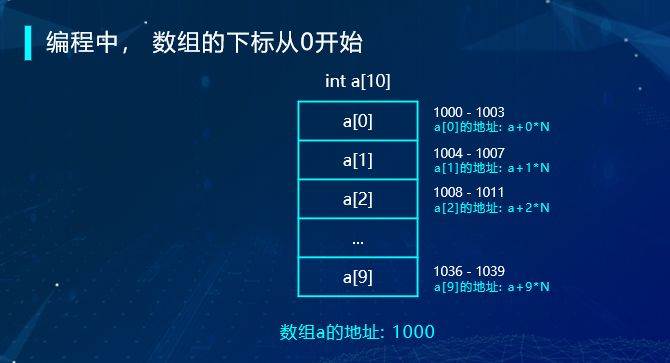
0在数学中起到至关重要的作用，有了0才可能有复数。0在数学中可以是占位符，在音乐中可以代表休止符等等……0的重要性还体现在可以使任何问题简单化，在编程中，数组的下标往往是从0开始的。

通过余数是否为0，可以将数字进行分组，如下图所示。

对此，我们可以引申思考一个问题——如果今天是星期天，那么100天之后是星期几？这个问题是编程中对日历相关问题处理时会经常遇到的，解题思路如下图所示。

但在计算机中，我们可以用更简单的方法——使用余数，可以将100个数除以7取余分成7组来判定，即余数为0时，代表100天后是星期日，余数为1时，代表100天后是星期一……余数为6时，代表100天后是星期六。

下面出一道稍微有点难度的题，大家可以根据提示思考，能理解了这个问题，就说明你已经完全掌握规律啦！

03

余弦定理和新闻分类

目前，大部分的新闻内容都由人工智能程序来写的。因此，媒体需要利用余弦定理来进行新闻分类，把财经、体育、娱乐等不同类型的文章对号入座。

如下图所示，计算机是读不懂新闻的，则会将文章通篇拆解为无数个汉字词，根据其出现的频率不同，呈现出不同的TF-IDF值，并用向量来表示每一篇文章的数据。如果两条向量的夹角越小，说明两篇文章的相似度越高，用词越接近。

而计算向量夹角，则会用到数学中的余弦定理。

04

神经网络中的数学基础

神经网络与人工智能息息相关，而人工智能中的绝大多数分支都与数学为基础。因此，学习编程能帮助我们深刻理解数学中的概念。

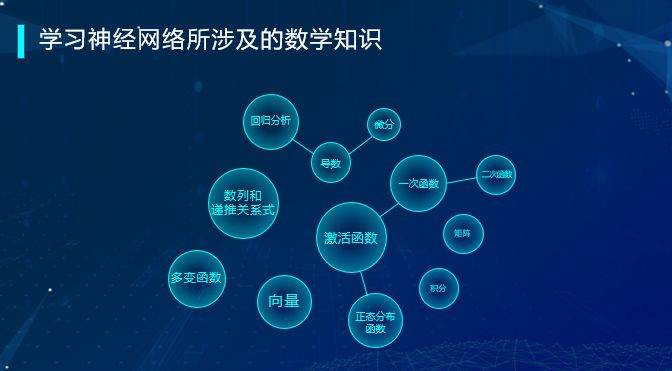
举例来说，神经网络中的神经元工作原理，可以简化为数学方法表达。

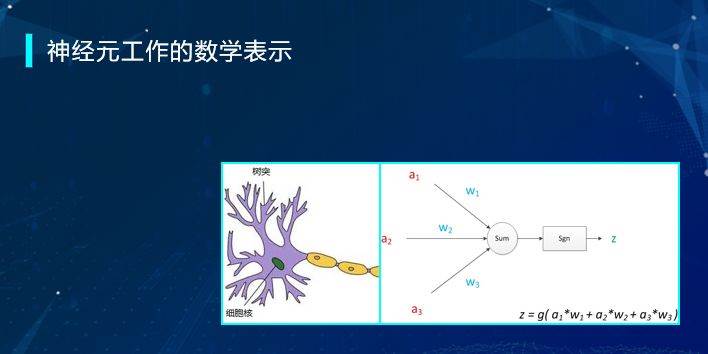
爱因斯坦说过，“宇宙最不可理解之处是它居然可以被理解。”这是因为我们的生活中所遇到的很多现象都可以用数学和编程方法来进行拆解从而理解的，这也正是数学的迷人之处，编程的迷人之处。